Définition du filtre
médian Marginal
La majorité des premiers travaux a concerné l’extension du filtre médian aux images couleur. Dans le cas des images en niveaux de gris, à chaque pixel est associé une valeur dans R et la relation < étant un ordre total sur R il est facile d’ordonner les valeurs d’un ensemble de pixels suivant cette relation d’ordre. Puisque chaque composante d’une image couleur peut être considérée comme une image en niveaux de gris, un filtre médian peut être appliqué sur chaque composante séparément. Ce type d’approche est appelé traitement marginal.
Grâce à sa simplicité, mais également à la souplesse de traitement qu'elle assure, cette méthode est utilisée avec succès dans de nombreux cas. Néanmoins, pour d'autre types d'applications, elle n'est pas pleinement satisfaisante, et ce, pour plusieurs raisons que nous allons voir.
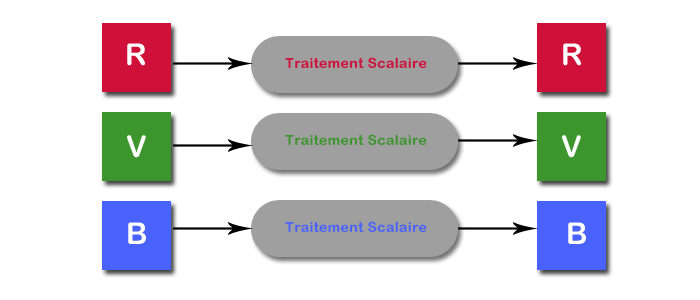
Traitement marginal sur les composantes d'un pixel
Limites du filtre
médian Marginal
De par sa structure, cette approche ignore totalement la dépendance pouvant exister entre les différentes composantes, délaissant ainsi une information pouvant participer à l’amélioration des performances des traitements. On peut également noter que cette stratégie demande autant de traitements qu'il y a de composantes, ce qui peut se révéler coûteux en temps de calcul lorsque le nombre de composantes est élevé.
L’intérêt de cette approche est qu’elle n’utilise que des traitements scalaires. Toutes les méthodes définies en imagerie monochrome sont alors directement exploitables, sans aucune adaptation.
On peut, bien évidemment, employer des traitements différents pour chaque composante, en fonction de la nature de ces composantes. Cette approche présente également des limites quant à la nature des traitements envisageables. Par exemple, une opération telle que le seuillage binaire ne peut se faire selon ce schéma, les M composantes binarisées ne fournissant généralement pas la même image binaire.
Le traitement marginal n’exploite pas la corrélation existante entre les différentes composantes (particulièrement importante pour le cas des images couleur) et peut provoquer l’apparition de fausses couleurs.
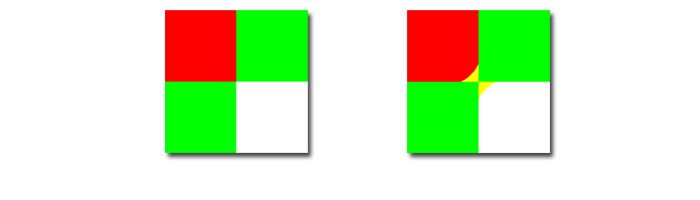
Fausses couleurs marginales
Solutions
aux limites
Un traitement vectoriel est donc plus approprié afin de prendre en compte la nature vectorielle des données. Cependant, cela nécessite la définition de nouveaux modèles pour l’extension des algorithmes scalaires au cas vectoriel. Le principal problème de ce genre d’extension repose sur la définition d’un ordre vectoriel approprié car il n’existe pas d’ordre naturel sur les vecteurs.
L'image obtenue après filtrage médian marginal fait apparaître une déformation des contours, typique du filtrage médian, ainsi qu'une région jaune indésirable).
Avec le filtre médian vectoriel, on retrouve bien sûr une déformation des angles due au filtrage médian, mais la couleur parasite jaune n'apparaît plus (cf onglet vectoriel).





