Morphologie
mathématique couleur
Les principaux opérateurs morphologiques reposent sur la définition des deux opérateurs de base que sont la dilatation et l’érosion.
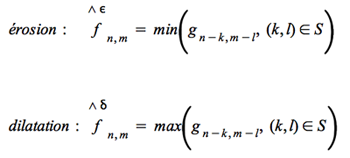
L'érosion permet de renforcer les zones sombres et d'éliminer les petits détails clairs.
La dilatation renforce les zones claires et élimine les petits détails sombres.
La morphologie demande donc la définition d’un ordre. On retrouve donc la situation évoquée lors de l’étude des filtres d’ordre.
Eléments
structurant
La morphologie mathématique repose sur l'utilisation d'un élément structurant. Un élément structurant est composée :
- d'un pixel central (en noir)
- d'un ensemble de pixels (en gris)
Voici un schéma montrant l'impact de l'élément structurant pour l'érosion et la dilatation :
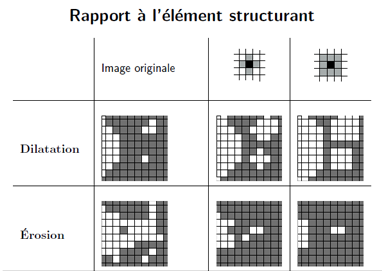
Impact de l'élément structurant
La dilatation et l'érosion ne sont pas des transformations inverses. Si l'on applique successivement une érosion puis une dilatation on ne retrouve pas l'image d'origine.
On appelle :
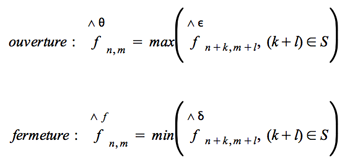
L'ouverture élimine les petits détails clairs.
La dilatation élimine les petits détails sombres.

Ouverture et fermeture
Approche
marginale
Bien sûr, comme nous l'avons déjà vu une solution simple et souvent utilisée consiste à traiter marginalement chacune des composantes. Cette manière de faire donne des résultats satisfaisants en général, mais le phénomène d’introduction de fausses couleurs, déjà évoqué, est beaucoup plus sensible qu'avec les filtres d'ordre.
La figure ci-dessous illustre ce phénomène.

Traitement marginal
Approche
vectorielle
Pour pouvoir définir correctement les opérateurs de morphologie couleur, il est nécessaire d’utiliser une relation d’ordre totale, qui assure que l'inf et le sup sont des vecteurs de l'ensemble de départ.
Une solution performante consiste alors à utiliser l'ordre par entrelacement de bits. Les opérateurs morphologiques couleur se définissent alors aisément, comme le montrent les deux exemples ci-dessous: dans l’ouverture, il n’y a plus d'apparition de fausses couleurs.

Traitement vectoriel





